How Much Information Has One Single Letter In An N-Gram?

Information content of single letter

Shannons Information-Theory is very concise when it comes about calculating the information content of a single letter a..z:

Source: https://de.wikipedia.org/wiki/Informationsgehalt 

So, when we know the appearance probability for a single letter, e.g. 'e', we can calculate its information content:

Source: https://de.wikipedia.org/wiki/Buchstabenhäufigkeit

So for example the delivered information of letter 'e' at the single appearance within the word 'household' can be calculated via:

But this information value does not respect the context of 'e' 's appearance. So if we regard another appearance of 'e' in the word 'enchiladas', the information content for 'e' would be the same 2.52 bit. 

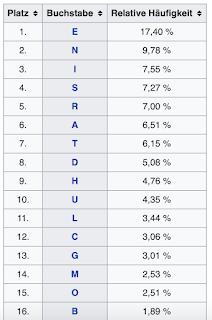
We can conclude: The information content calculation is based on the median appearance probability of the single isolated letter 'e' over a huge german text corpus (~17,4%).

Information content of a trigramm

If the letters within a language would appear independent of each other, then the appearance probability of a tri-gramm e.g. "die" could easily be calculated from the single-letter-appearance-probabilities "d", "i" and "e" by multiplication:

But it shows this is not the case: 

Source: https://de.wikipedia.org/wiki/N-Gramm

This is due to correlation between the letters, called language redundancy. So with growing observation window size N, you get less and less information per letter, due to growing incorporated redundancy between letters.

So to correctly calculate the information content of a trigram you have to use the trigram probability:

Information of single letter contained within n-gram at position x

Now we want to answer the question from the headline: How can we calculate the information content of letter 'e' when contained and observed within a window of size 3, i.e. within an 3-gram?

Or to be even more exact: What's the information delivered by letter 'e' at position 2 (or 1 or 0) within a 3-gram?

Answer:

Step 0: get a file with all 3-gram frequencies (or alternatively absolute frequencies) in your language

Step 1: find all 3-grams where 'e' appears at position 2 (last position)

Step 2: Calculate the trigram-information content for every trigram and sum them up

Step 3: divide by 3, because that's the 'share belonging to 'e'' - every letter, that is part of the 3-gram get's the same 'share', i.e. a third

Code / Jupyter-Notebook

Source: https://github.com/hahnburg/redundancyandstructure/blob/master/4_Strukturelle_Redundanz_de.ipynb